Using hyperbolic cosine calculator in batch processing
APP description
A hyperbolic cosine function is a type of hyperbolic function. We know that the trigonometric function is divided into six types: sine sin, cosine cos, tangent tan, cotangent cot, secant sec, and cosecant csc. Then, similarly, hyperbolic functions are also divided into six types: hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cotangent, hyperbolic secant, and hyperbolic cosecant. The hyperbolic cosine function is also one of them. The hyperbolic cosine function is called cosh, or it can be abbreviated as ch.
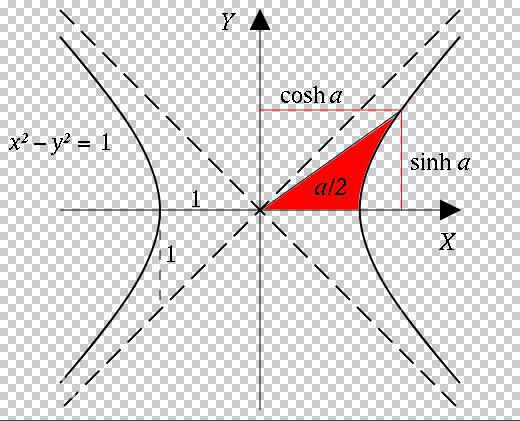
The ray emitted from the origin intersects the unit hyperbola (equation :) at the point (cosh a, sinh a). Here a is twice the area enclosed by the ray, hyperbola, and x-axis. For points on the hyperbola below the x-axis, this area is considered negative. Among them, cosh a is the hyperbolic cosine function of a. After complex calculations can be derived:

Usage example
Enter values: 5, 6, 7
Click "Calculate" and output the result
Hyperbolic cosine:
74.209949
201.715636
548.317035
Note
Values are separated by (,) or a set of data per line