Projection coordinate system PCS (Projection Coordinate System), which is also called non-Earth projection coordinate system (notearth), or simply called plane coordinate system. That is to use the coordinate system based on X and Y values to describe the position of a point on the earth.

What is the relationship between the projection coordinate system and the previous geographic coordinate system? In fact, the geographical coordinate system is spherical coordinates, the reference surface is ellipsoid, the coordinate unit is longitude and latitude, while the projection coordinate system is the plane coordinate system, the reference plane is the horizontal plane, the coordinate unit is meter, kilometer and so on.

What is projection?

Projection refers to using a set of light to project the shape of an object onto a plane, called projection, which we call the projection plane, and look at the following picture, and we want to learn the projection, the object to be projected is the earth.

The surface that can be expanded into a plane is the plane itself, and the ball can never be expanded into a plane, so we can only make the ball into a plane by projection, and there are many ways of projection of the ball.

Why do you need projection?

The projection is required because the longitude and latitude in the geographic coordinate system do not have a unit, and the degree, minute and second are only a decimal system. In addition, the same is 1 degree longitude. The arc length expressed in different latitude zones is different, which brings difficulties to the area and quantitative calculation.

Traditional maps (compared with 3D platforms such as Google Earth) are presented on a two-dimensional plane, so we need a mapping method that can convert the three-dimensional coordinates on the earth's sphere to a two-dimensional plane. This method is map projection. Therefore, map projection is a mapping method from longitude and latitude B, L, H to projection coordinates X, Y, Z.

The essence of map projection is to establish the corresponding relationship between the points on the surface of the earth's ellipsoid and the points on the map plane, and convert the longitude and latitude coordinates under the geographical coordinate system established on the sphere into the rectangular coordinates on the plane through a projection method.

The purpose of map projection is to establish a plane coordinate system (called projection coordinate system). Many calculations and operations are simpler on the plane than on the surface.

For example, on the sphere, two points with the same latitude and the same longitude difference have different distances at different latitudes, which brings inconvenience to the calculation. This problem does not exist on the Euclidean plane.

Many classic GIS software, such as ArcMap, have basic framework, including rendering, editing and other functions developed based on 2D plane, which is also consistent with our requirements for maps.

In the range of allowable deformation, a unified plane coordinate system is established, which is emphasized because the range of the map is also an important factor to be considered when designing the map projection.

Classification of projections

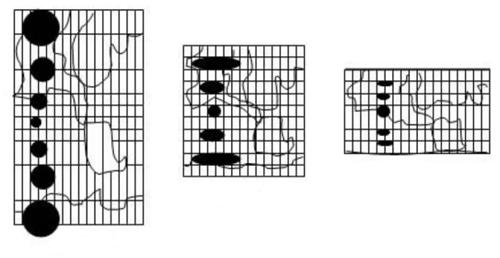
If the target on the sphere is flattened to the plane, the target will certainly be compressed or stretched. According to the nature of deformation, map projection can be divided into the following categories.

• Isometric projection: after projection, the deformation of the target is consistent in all directions, and the overall angle remains unchanged.

• Isometric projection: the overall length remains unchanged after projection, and the area and angle are somewhat deformed.

• Equal area projection: assume that there is a differential circle on the target. If the area of the circle remains the same after the projection, the projection is equal area projection.

• Arbitrary projection: a projection in which the area, angle, and length change after projection.

The figure below is as follows:

According to the way of projection, it can be divided into the following categories

• Cylindrical projection: the projection plane is a cylinder
• Conical projection: the projection plane is a cone
• Azimuth projection: the projection plane is flat

Then according to the relative position of the principal axis of the projection plane (cylinder, cone, plane) and the earth axis (the short axis connecting the north and south poles), the projection can be divided into the following ways:

• Positive axis projection: the central axis of the projection plane coincides with the earth axis
• Oblique projection: oblique intersection of the central axis of the projection plane and the earth axis
• Horizontal axis projection: the central axis of the projection plane is perpendicular to the earth axis
• Tangent projection: the projection plane is tangent to the ellipsoid
• Secant projection: the projection plane is cut from the ellipsoid

Common projection methods

Mercator projection-Mercator

Mercator projection, also known as Mercator projection and isometric cylindrical projection, was created by Dutch cartographer G. Mercator in 1569.

Simply put, suppose that the earth is enclosed in a cylinder, and the equator is tangent to the cylinder, then put a lamp in the center of the earth, project the figure on the sphere onto the cylinder, and then expand the cylinder to form a world map with Mercator projection, as shown below:

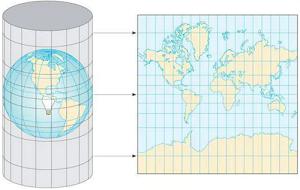
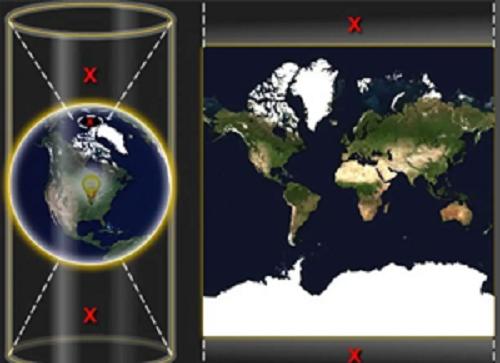
Because it can show the correct orientation between any two points, most of the nautical charts and route charts are drawn in this way, and the linear scale of this projection remains unchanged around any point in the map. thus, the angle and shape of the continental outline can be kept unchanged (that is, equal angle), but the Mercator projection will deform the area, and the proportion of poles (that is, the South and Arctic regions) will even reach infinity.

So it does not fully show the whole world, the highest latitude on the map is 85.05 degrees, in order to simplify the calculation, using spherical mapping, rather than ellipsoidal shape, using Mercator projection is just to facilitate the display of the map, we also need to know that this mapping will bring 0.33% error to the Y axis, as shown in the following figure

Gaussian Kruger projection (Gauss-Kruger)

This projection was drawn up by German mathematician, physicist and astronomer Gauss in the 1920s, and then supplemented by German geodesy Krueger in 1912, so it is called Gaussian Krueger projection.

You can imagine an elliptical cylinder lying horizontally on the ellipsoid of the earth (tangent to the meridian coil), rotating around the earth's axis, projecting the earth's surface onto the elliptical cylinder, projecting it onto the elliptical cylinder, and then cutting and spreading it into a plane along the height of the elliptical cylinder, as shown below.

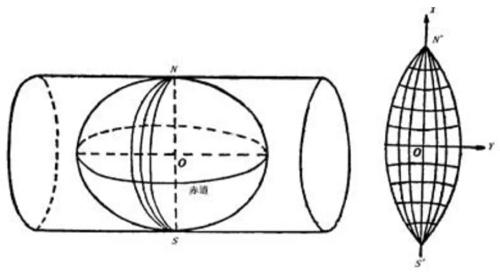
The longitude is 180 degrees from east to west, and one is peeled off by 3 or 6 degrees to project this so-called zoning. By rotating the projection plane of Gauss Kruger, you can obtain the projection of the next zoning to fit all parts of the world, as shown in the following figure.

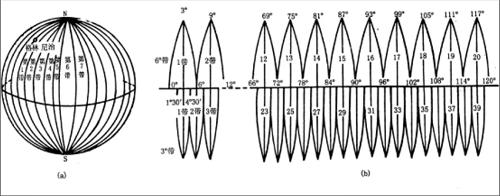
Gaussian Kruger projection, also known as equiangular transverse elliptical cylindrical projection, is called transverse Mercator projection in British and American countries. The global / general transverse Mercator projection (UTM) used by the United States in compiling military maps and satellite images of earth resources around the world is a kind of deformation of transverse Mercator projection.

Universal Transverse Mercator projection (UTM)

UTM full name Universal Transverse Mercator is called universal transverse Mercator projection in Chinese, which is very similar to Gauss Krueger projection, except that it is not tangent to the meridian coil, but to cut the earth ellipsoid on the transverse axis of the ellipsoid (passing through the earth). The center line of the ellipsoid lies on the equatorial plane of the ellipsoid and passes through the ellipsoid body point, thus projecting the point on the ellipsoid onto the ellipsoid, as the following:

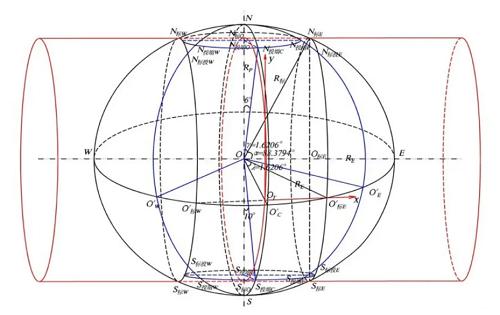
This kind of projection was put forward by the U.S. Army Engineering surveying and Mapping Bureau in the 1940s. Clarke 1866 ellipsoid is used in the United States and WGS84 ellipsoid is used in other parts of the world. At present, most remote sensing images use the projection coordinate system projected by UTM.

Network Mercator projection (WebMercator)

Network Mercator projection is called PVPM (Popular Visualization Pseudo Mercator) in English. It is not a strict Mercator projection, but a pseudo Mercator projection method, which was first proposed by Google Map.

Its lack of rigor is that in the process of projection, the ellipsoid representing the earth is treated as a positive sphere. Legend has it that Google programmers don't bother to use ellipsoids to program and calculate screen coordinates. It takes the whole world equator as the standard latitude, the prime meridian as the central meridian, the intersection point as the coordinate origin, positive to east to north and negative to west to south.

We mentioned the Mercator projection method above, so we can know that when the latitude approaches the poles, the value of y tends to be infinite, so these lazy engineers limit the range of values of the Y axis to [- 20037508.3427892me 20037508.3427892].

Electronic maps usually show geographical coordinates in units of longitude and latitude, while Mercator projection coordinates longitude range: [- 180180], latitude is known to be impossible to reach 90 °, the value range is [- 85.05112877980659], what about the rest of the area? No one knows. Leave it alone if you don't need it. In addition, we also need to know that the WebMercator projection also uses the WGS84 datum. For datum correlation, please see the geographic coordinate system above.

The commonly used PCS family of Gaussian Kruger projection, in China, the geographical coordinate system is only Beijing 54, Xi'an 80, and country 2000, which can be selected according to the needs of the central longitude.

The PCS family based on UTM projection is similar to the family of Gaussian Kruger projection coordinate system, except that it is only based on WGS84 and can be selected according to the needs of the central longitude. China's Gao de, Baidu, Tencent Map, Google Maps and OSM Maps all use the network Mercator to display flatly, but the geographic coordinate systems of domestic Gao de Baidu Tencent and domestic Google Maps are encrypted, and although Sky Map uses the national 2000 geographic coordinate system, it also provides a Mercator projection method to display plane maps, while ArcGIS Earth is similar to Google Earth by directly using 3857 coordinates.