5.28. The basis and representation of Graph Theory

5.28.1. I. the concept and its introduction ¶

Graph theory (Graph Theory) is a branch of discrete mathematics and a branch of Graph.

A graph is a mathematical structure used to model pairwise relationships between objects. It consists of “nodes” or “Vertex” and “Edge” that connect these vertices.

It is worth noting that the set of vertices of a graph cannot be empty, but the set of edges can be empty. The graph may be undirected, which means that the edges in the graph do not need to distinguish directions when connecting vertices. Otherwise, the graph is said to be directed. The left graph below is a typical undirected graph structure, and the right graph is a directed graph. The graphs introduced in this chapter are all undirected graphs.

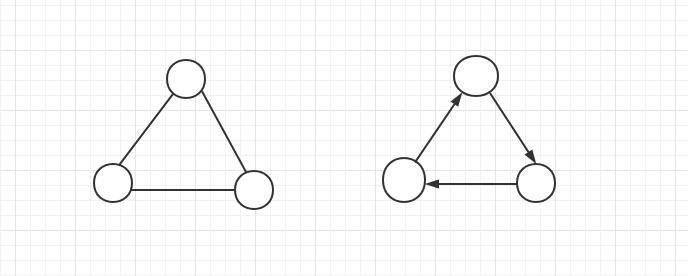
Classification of graphs: unauthorized graphs and weighted graphs, whether the edges of connecting nodes and nodes have numerical values corresponding to them, some are weighted graphs, otherwise they are unauthorized graphs.

图的连通性： In graph theory, connected graphs are based on the concept of connectivity. In an undirected graph G, if there is a path from vertex I to vertex j (of course, there must be a path from j to I), then I and j are said to be connected. If G is a digraph, then all edges in the path connecting I and j must be in the same direction. If any two points in a graph are connected, then the graph is called a connected graph. If this graph is a directed graph, it is called a strongly connected graph (note: both directions are required). The connectivity of a graph is the basic property of a graph.

完全图： It is a simple undirected graph, in which each pair of different vertices is connected by an edge.

自环边： The beginning and end of an edge is a point.

平行边： There are multiple edges connected between the two vertices.

5.28.2. II. Applicable instructions ¶

Graphs can be used to model many types of relationships and processes in physical, biological, social, and information systems, and many practical problems can be represented by diagrams. Therefore, graph theory has become a powerful mathematical tool in many disciplines, such as operational research, cybernetics, information theory, network theory, game theory, physics, chemistry, biology, social sciences, linguistics, computer science and so on. When emphasizing its application to real-world systems, a network is sometimes defined as a graph in which the relationship between attributes (such as names) is associated in the form of nodes and or edges.

5.28.3. Third, the expression form of the graph ¶

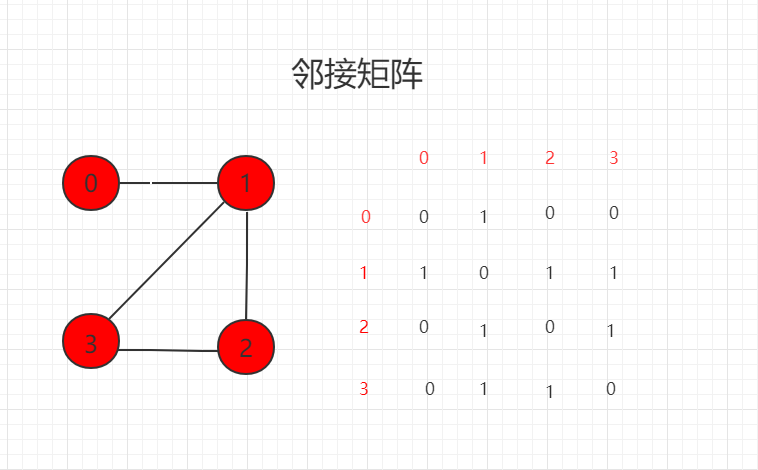
邻接矩阵： 1 means connected, 0 means not connected.

邻接表： Express only the vertex information connected to the vertex

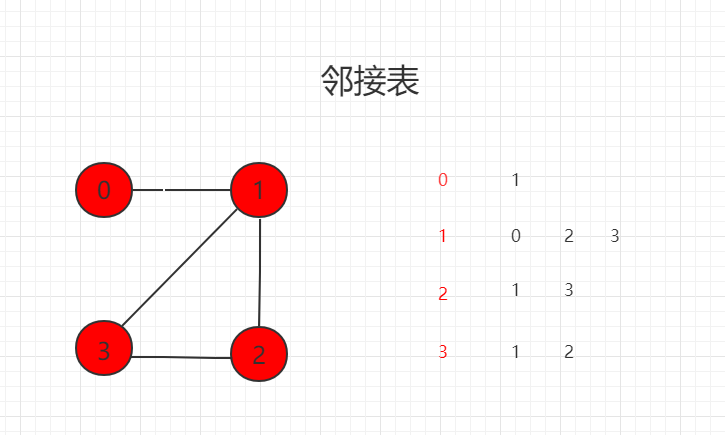
Adjacency tables are suitable for representing sparse graphs (Sparse Graph)

The adjacency matrix is suitable for representing dense graphs (Dense Graph).

5.28.4. Java instance code ¶

源码包下载： Download

(1) 邻接矩阵

package runoob.graph;
/*\*
 \* 邻接矩阵
 */
public class DenseGraph {
    // 节点数
    private int n;
    // 边数
    private int m;
    // 是否为有向图
    private boolean directed;
    // 图的具体数据
    private boolean[][] g;
    // 构造函数
    public DenseGraph( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;
        this.directed = directed;
        // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false,
表示没有任和边
        // false为boolean型变量的默认值
        g = new boolean[n][n];
    }
    // 返回节点个数
    public int V(){ return n;}
    // 返回边的个数
    public int E(){ return m;}
    // 向图中添加一个边
    public void addEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        if( hasEdge( v , w ) )
            return;
        g[v][w] = true;
        if( !directed )
            g[w][v] = true;
        m ++;
    }
    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        return g[v][w];
    }
}

package runoob.graph;
import java.util.Vector;
/*\*
 \* 邻接表
 */
public class SparseGraph {
    // 节点数
    private int n;
    // 边数
    private int m;
    // 是否为有向图
    private boolean directed;
    // 图的具体数据
    private Vector<Integer>[] g;
    // 构造函数
    public SparseGraph( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;
        this.directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = (Vector<Integer>[])new Vector[n];
        for(int i = 0 ; i < n ; i ++)
            g[i] = new Vector<Integer>();
    }
    // 返回节点个数
    public int V(){ return n;}
    // 返回边的个数
    public int E(){ return m;}
    // 向图中添加一个边
    public void addEdge( int v, int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        g[v].add(w);
        if( v != w && !directed )
            g[w].add(v);
        m ++;
    }
    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v].elementAt(i) == w )
                return true;
        return false;
    }
}