5.6.1. I. the concept and its introduction ¶
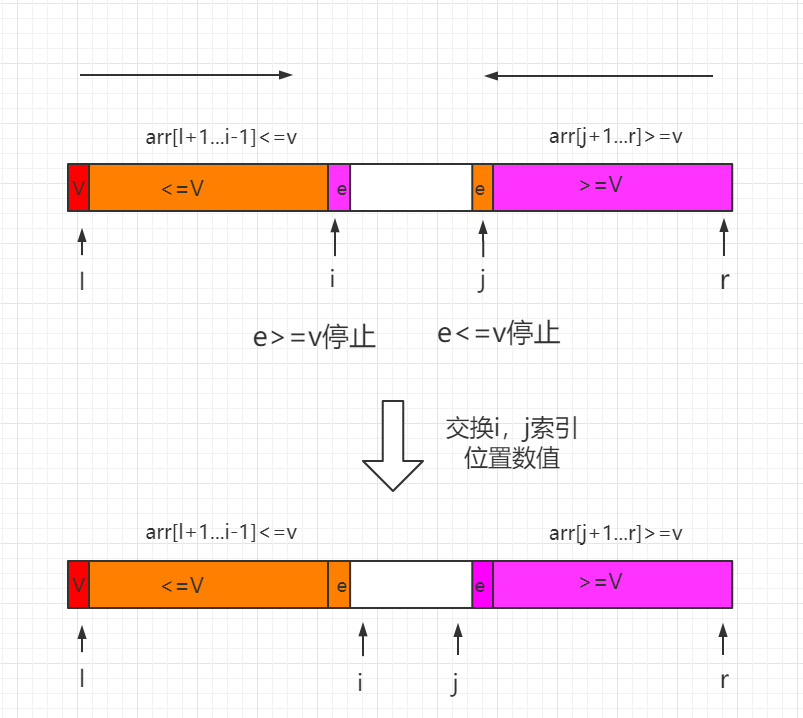
The two-way quick sort algorithm is an improved version of randomized quick sort. The partition process uses two index values (I, j) to traverse the array, setting the <v To the left of the location pointed to by index I, and set the >v Is placed to the right of the location pointed to by index j v Represents the specified value.
5.6.2. II. Applicable instructions ¶
Time and space complexity are the same as randomized quick sorting. For arrays with a large number of repetitive elements, the efficiency of randomized quick sorting in the previous section is very low, resulting in extreme imbalance in the length of subarrays that are larger than or less than the base point data after partition, and even degenerate to O (n = 2) time complexity algorithms. In this case, two-way quick sorting algorithm can be used.
5.6.3. III. Process diagram ¶
Use two index values (I, j) to traverse our sequence, setting the <=v To the left of the location pointed to by index I, and set the >=v Is placed to the right of the location pointed to by index j, balancing the left and right subarrays
5.6.4. 4. Java instance code ¶
源码包下载: Download QuickSort2Ways.java file code: ¶
package runoob;
/*\*
\* 双路快速排序
*/
public class QuickSort2Ways {
//核心代码---开始
private static int partition(Comparable[] arr, int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr, l , (int)(Math.random()\*(r-l+1))+l );
Comparable v = arr[l];
// arr[l+1...i) <= v; arr(j...r] >= v
int i = l+1, j = r;
while( true ){
while( i <= r && arr[i].compareTo(v) < 0 )
i ++;
while( j >= l+1 && arr[j].compareTo(v) > 0 )
j --;
if( i > j )
break;
swap( arr, i, j );
i ++;
j --;
}
swap(arr, l, j);
return j;
}
//核心代码---结束
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if (l >= r) {
return;
}
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试 QuickSort
public static void main(String[] args) {
// 双路快速排序算法也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
// Quick Sort也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0,
100000);
sort(arr);
SortTestHelper.printArray(arr);
}
}