5.5.1. I. the concept and its introduction ¶
Quick sorting was proposed by C. A. R. Hoare in 1960.
随机化快速排序基本思想: The data to be sorted is divided into two independent parts through a sort, and all the data in one part is smaller than all the data in the other part, and then the two parts of data are sorted quickly according to this method. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.
5.5.2. II. Applicable instructions ¶
Quick sort is a relatively fast sorting algorithm, and its average running time is O (nlogn). The reason why it is particularly fast is due to very concise and highly optimized internal loops, and the worst-case performance is O (n ^ 2). Like merging, quick sorting is a recursive algorithm of divide and conquer. From the perspective of spatial performance, quick sorting only needs the auxiliary space of one element, but quick sorting needs a stack space to achieve recursion, and the space complexity is also O (logn).
5.5.3. III. Process diagram ¶
Select a base point in an array, such as 4 in the first position, then move 4 to the correct position so that the data in the previous subarray is less than 4, and the data in the subsequent subarray is greater than 4, and then gradually recursively to complete the entire sort.
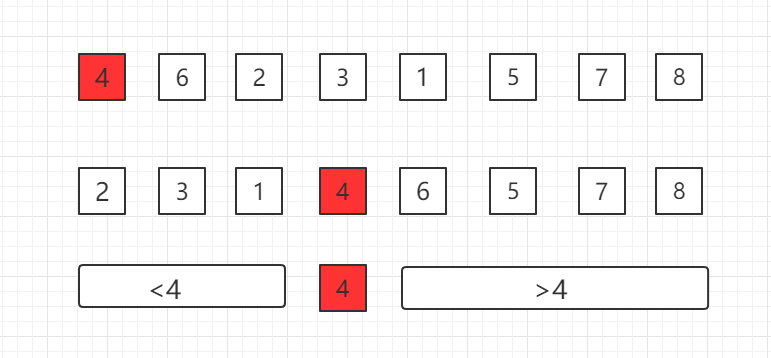
How to move the selected base point data to the correct location is the core of quick sorting, which we call Partition.
The process is as follows, where I is the element location of the current traversal comparison:
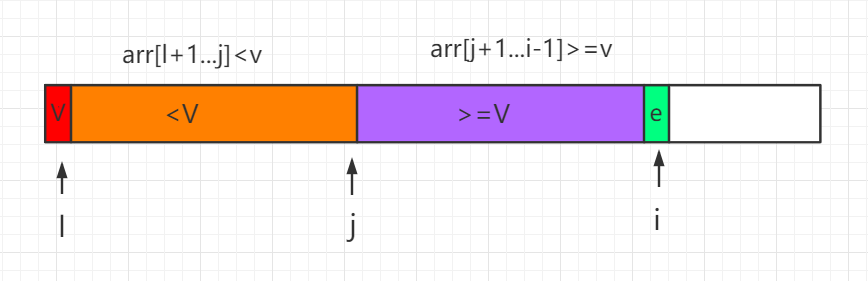
This partition process is represented in code as follows: If the almost ordered array is sorted quickly, the size of the subarray is extremely unbalanced after each partition partition, and it is easy to degenerate to O (n ^ 2) time complexity algorithm. We need to optimize the above code and randomly select a base point for comparison, which is called randomized quick sorting algorithm. Just add the following line before the above code and randomly select one of the data in the array and the base point data to exchange.Example ¶
private static int partition(Comparable[] arr, int l, int r){
Comparable v = arr[l];
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
//数组元素位置交换
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
5.5.4. 4. Java instance code ¶
源码包下载: Download QuickSort.java file code: ¶
package runoob;
/*\*
\* 随机化快速排序
*/
public class QuickSort {
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(Comparable[] arr, int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr, l , (int)(Math.random()\*(r-l+1))+l );
Comparable v = arr[l];
// arr[l+1...j] < v ; arr[j+1...i) > v
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if (l >= r) {
return;
}
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试 QuickSort
public static void main(String[] args) {
// Quick Sort也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0,
100000);
sort(arr);
SortTestHelper.printArray(arr);
}
}