5.12.1. I. the concept and its introduction ¶
Heap sorting (Heapsort) is a sort algorithm designed by using the data structure of heap.
The heap is a structure similar to a complete binary tree and satisfies the property of stacking at the same time, that is, the key value or index of a child node is always less than (or greater than) its parent node.
5.12.2. II. Applicable instructions ¶
Our previous process of constructing a heap is to call the insert method one by one and insert it into the heap one by one using shift up. The time complexity of this algorithm is O (nlogn). This section describes a process of constructing heap sorting, called Heapify The time complexity of the algorithm is O(n) .
5.12.3. III. Process diagram ¶
A complete binary tree has an important property. For the first non-leaf node, the index is n/2 The index value obtained by taking an integer, where n Is the number of elements (provided that the array index starts at 1).
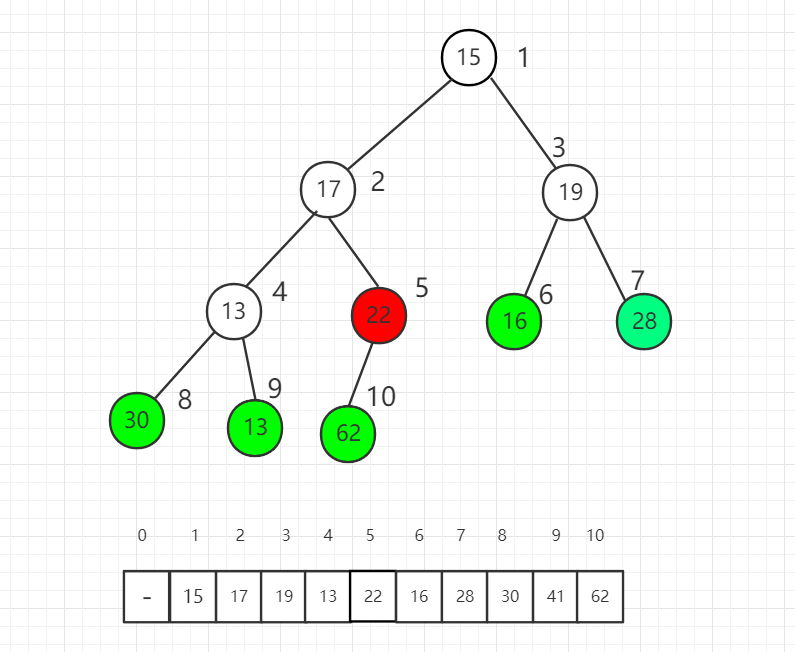
Index 5 is the first non-leaf node, from which we shift down each element as the root node one by one to satisfy the nature of the maximum heap.
After the shift down operation is performed on the index 5 position, 22 and 62 switch positions.
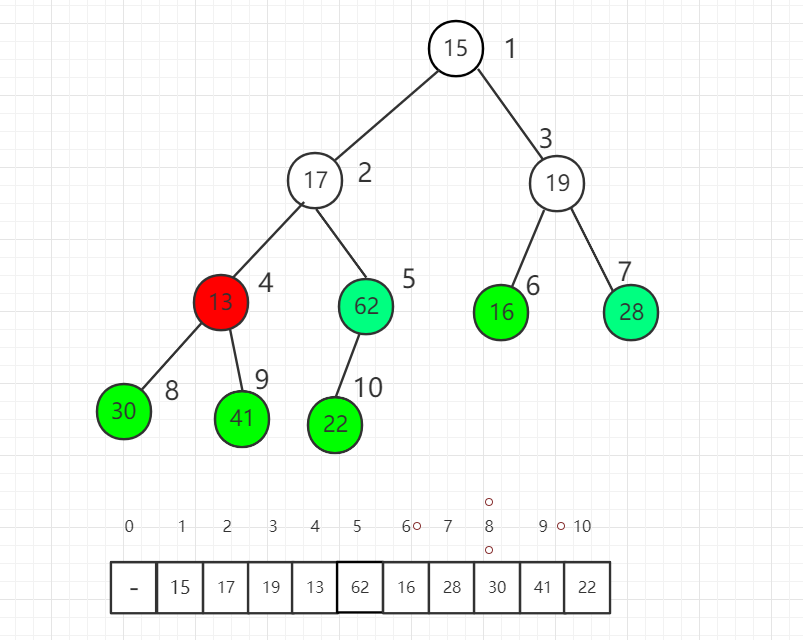
Shift down index 4 elements
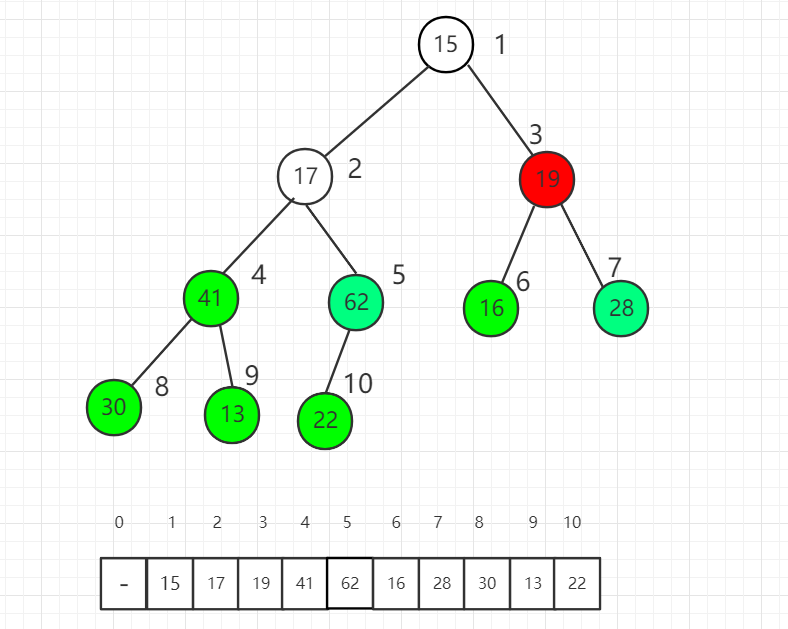
Shift down index 3 elements
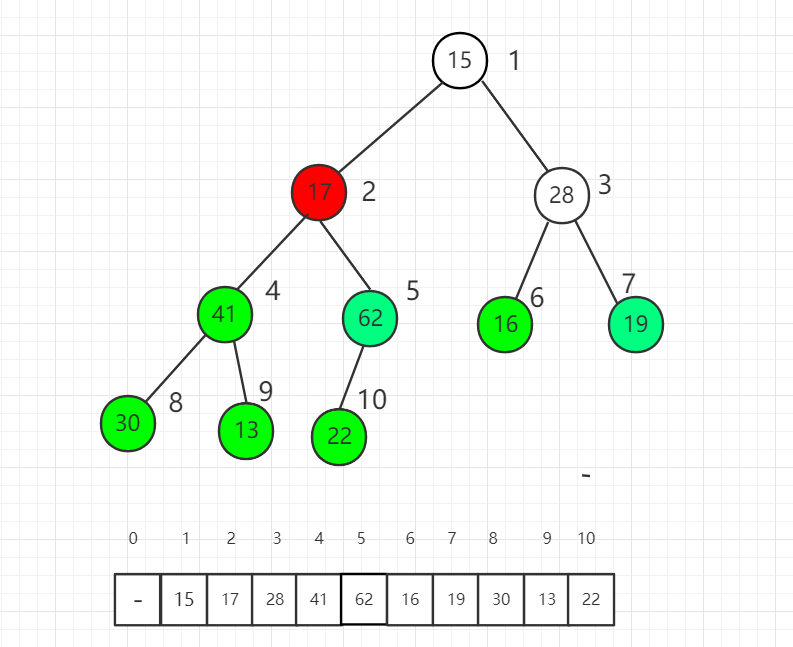
Shift down the index 2 element
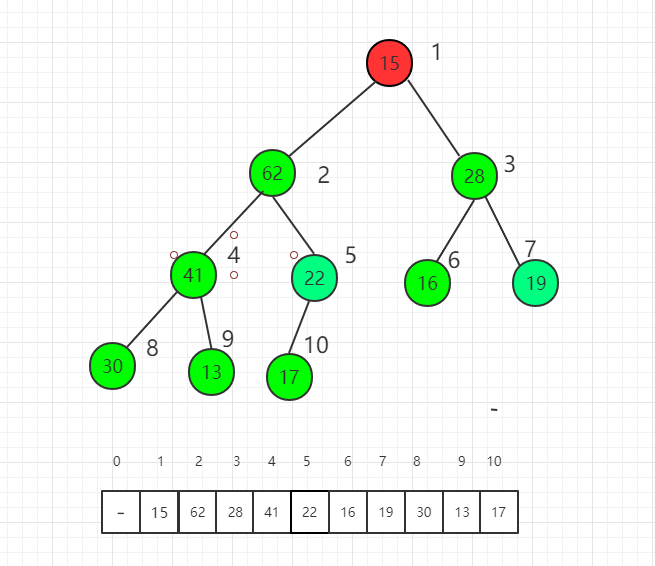
Finally, shift down the root node, and the whole heap sorting process is completed.
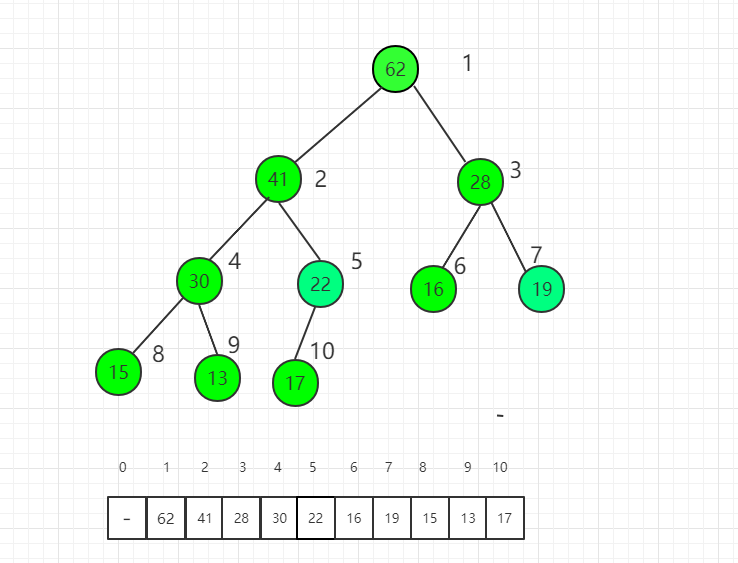
5.12.4. 4. Java instance code ¶
源码包下载: Download Src/runoob/heap/Heapify.java file code: ¶
package runoob.heap;
import runoob.sort.SortTestHelper;
/*\*
\* 用heapify进行堆排序
*/
public class Heapify<T extends Comparable> {
protected T[] data;
protected int count;
protected int capacity;
// 构造函数, 通过一个给定数组创建一个最大堆
// 该构造堆的过程, 时间复杂度为O(n)
public Heapify(T arr[]){
int n = arr.length;
data = (T[])new Comparable[n+1];
capacity = n;
for( int i = 0 ; i < n ; i ++ )
data[i+1] = arr[i];
count = n;
//从第一个不是叶子节点的元素开始
for( int i = count/2 ; i >= 1 ; i -- )
shiftDown(i);
}
// 返回堆中的元素个数
public int size(){
return count;
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty(){
return count == 0;
}
// 像最大堆中插入一个新的元素 item
public void insert(T item){
assert count + 1 <= capacity;
data[count+1] = item;
count ++;
shiftUp(count);
}
// 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
public T extractMax(){
assert count > 0;
T ret = data[1];
swap( 1 , count );
count --;
shiftDown(1);
return ret;
}
// 获取最大堆中的堆顶元素
public T getMax(){
assert( count > 0 );
return data[1];
}
// 交换堆中索引为i和j的两个元素
private void swap(int i, int j){
T t = data[i];
data[i] = data[j];
data[j] = t;
}
//*******************\*
//\* 最大堆核心辅助函数
//*******************\*
private void shiftUp(int k){
while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
swap(k, k/2);
k /= 2;
}
}
private void shiftDown(int k){
while( 2\*k <= count ){
int j = 2\*k; // 在此轮循环中,data[k]和data[j]交换位置
if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
j ++;
// data[j] 是 data[2*k]和data[2*k+1]中的最大值
if( data[k].compareTo(data[j]) >= 0 ) break;
swap(k, j);
k = j;
}
}
// 测试 heapify
public static void main(String[] args) {
int N = 100;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0,
100000);
Heapify<Integer> heapify = new Heapify<Integer>(arr);
// 将heapify中的数据逐渐使用extractMax取出来
// 取出来的顺序应该是按照从大到小的顺序取出来的
for( int i = 0 ; i < N ; i ++ ){
arr[i] = heapify.extractMax();
System.out.print(arr[i] + " ");
}
// 确保arr数组是从大到小排列的
for( int i = 1 ; i < N ; i ++ )
assert arr[i-1] >= arr[i];
}
}