5.30. Depth-first traversal and connected components

The main idea of depth-first traversal (Depth First Search) is to start with an unvisited vertex and walk along the edge of the current vertex to the unvisited vertex. When there are no unvisited vertices, go back to the previous vertex and continue to explore other vertices until all the vertices have been visited.

The figure of the following example is traversed from 0 as shown in the figure on the right:

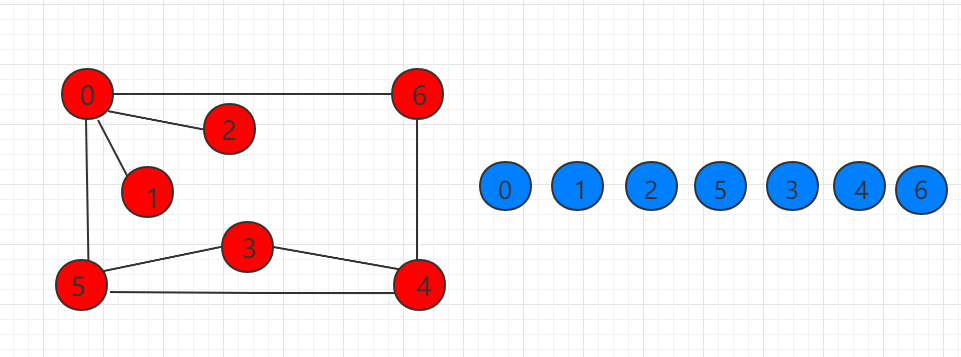
A polar Dalian connected subgraph of an undirected graph G is called a connected component (or connected branch) of G. A connected graph has only one connected component, that is, itself, and an unconnected undirected graph has multiple connected components. There is no edge connection between the connected component and the connected component. Depth-first traversal can be used to find connected components.

The following is to find the connected components as an example to achieve the depth-first traversal of the graph, called dfs. In the following code snippet, the visited array records whether the node is accessed during the dfs process, the ccount records the number of Unicom components, the id array represents the Unicom component mark corresponding to each node, and the two nodes have the same id value to indicate that they belong to the same Unicom component.

...
// 构造函数, 求出无权图的联通分量
public Components(Graph graph){
    // 算法初始化
    G = graph;
    visited = new boolean[G.V()];
    id = new int[G.V()];
    ccount = 0;
    for( int i = 0 ; i < G.V() ; i ++ ){
        visited[i] = false;
        id[i] = -1;
    }
    // 求图的联通分量
    for( int i = 0 ; i < G.V() ; i ++ )
        if( !visited[i] ){
            dfs(i);
            ccount ++;
        }
}
...

The depth-first traversal of the graph is a recursive process, which implements the code:

...
// 图的深度优先遍历
void dfs( int v ){
    visited[v] = true;
    id[v] = ccount;
    for( int i: G.adj(v) ){
        if( !visited[i] )
            dfs(i);
    }
}
...

package runoob.graph;
import runoob.graph.read.Graph;
/*\*
 \* 深度优先遍历
 */
public class Components {
    Graph G;                    // 图的引用
    private boolean[] visited;  // 记录dfs的过程中节点是否被访问
    private int ccount;         // 记录联通分量个数
    private int[] id;           // 每个节点所对应的联通分量标记
    // 图的深度优先遍历
    void dfs( int v ){
        visited[v] = true;
        id[v] = ccount;
        for( int i: G.adj(v) ){
            if( !visited[i] )
                dfs(i);
        }
    }
    // 构造函数, 求出无权图的联通分量
    public Components(Graph graph){
        // 算法初始化
        G = graph;
        visited = new boolean[G.V()];
        id = new int[G.V()];
        ccount = 0;
        for( int i = 0 ; i < G.V() ; i ++ ){
            visited[i] = false;
            id[i] = -1;
        }
        // 求图的联通分量
        for( int i = 0 ; i < G.V() ; i ++ )
            if( !visited[i] ){
                dfs(i);
                ccount ++;
            }
    }
    // 返回图的联通分量个数
    int count(){
        return ccount;
    }
    // 查询点v和点w是否联通
    boolean isConnected( int v , int w ){
        assert v >= 0 && v < G.V();
        assert w >= 0 && w < G.V();
        return id[v] == id[w];
    }
}