This section describes how to find the minimum and maximum values and delete the minimum and maximum values before deleting the binary search tree node.
Take the minimum as an example (the maximum is the same):
Find the minimum key value code logic and go to the left child node to find it recursively:
...
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
if( node.left == null )
return node;
return minimum(node.left);
}
...
Delete the minimum key value of the binary search tree. If the node does not have a right subtree, delete it directly. If there is a right subtree, as shown in the figure:
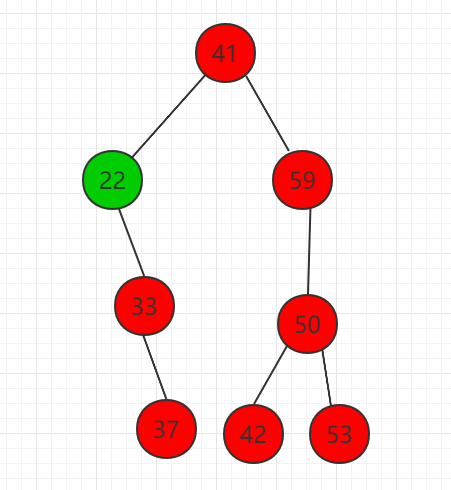
Delete node 22, there is a right child, just replace node 22 with 33 nodes in the right subtree.
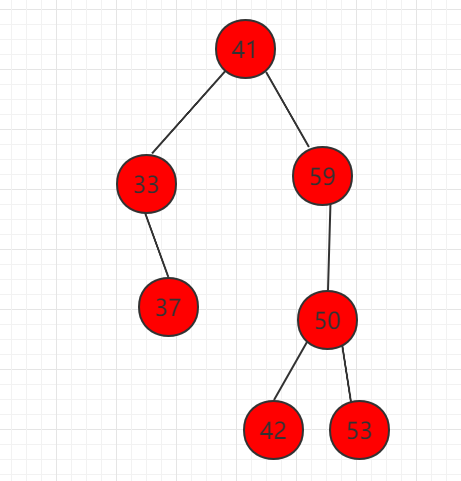
The minimum value of this deletion is represented by the code:
...
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
...
Now let’s discuss the following three cases of node deletion in the binary search tree:
1、 Delete the node with only the child on the left, as shown in node 58 below.
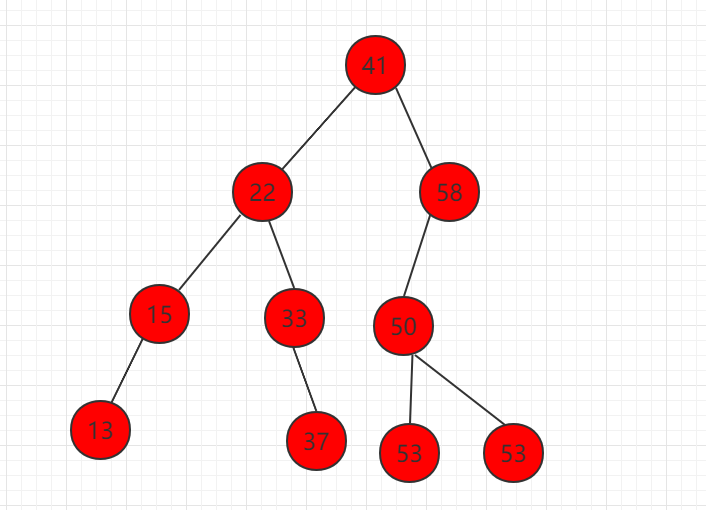
Delete element 58, let the left subtree directly replace the position of 58, the nature of the whole binary search tree remains the same.
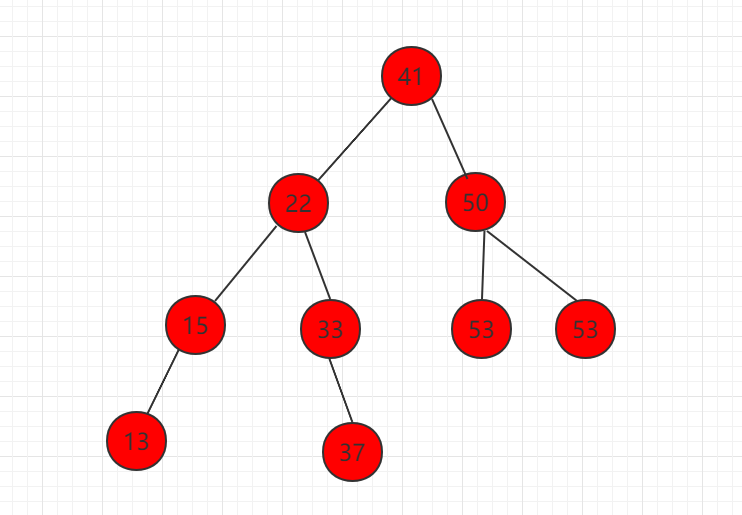
2、 Delete the node with only the right child, as shown in node 58 below.
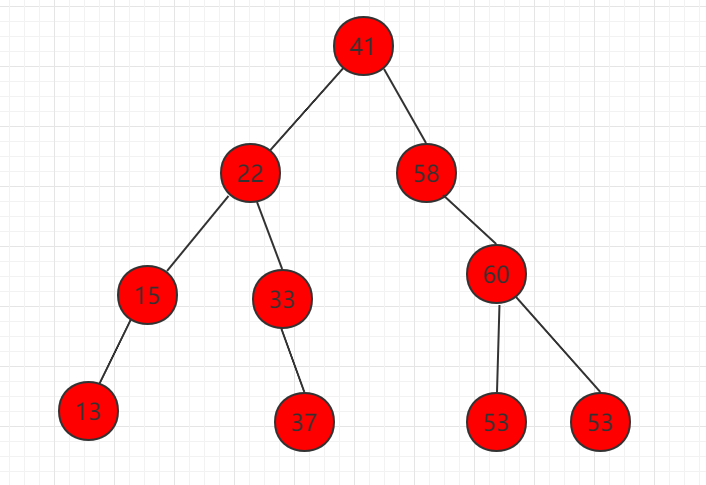
Delete element 58, let the right subtree directly replace the position of 58, the nature of the whole binary search tree remains the same.
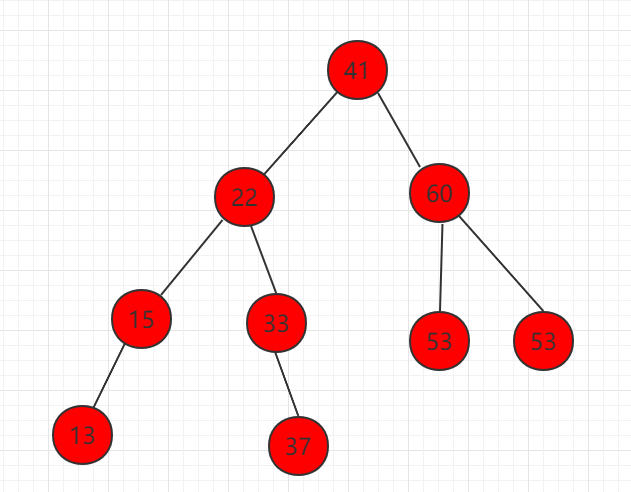
3、 Delete nodes with children on the left and right, as shown in node 58 below.
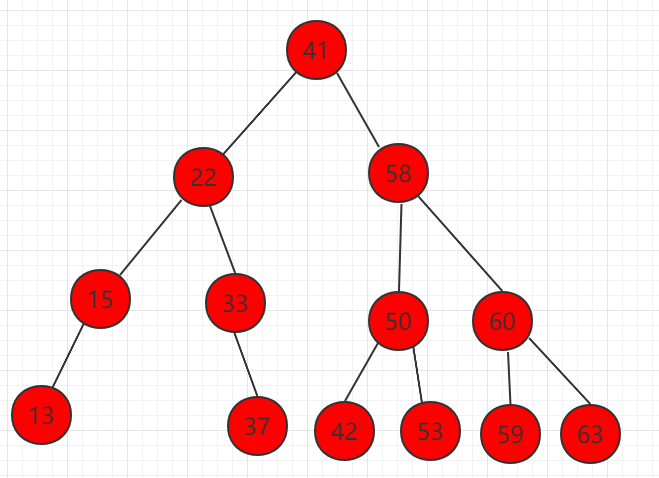
(1)找到右子树中的最小值,为节点 59
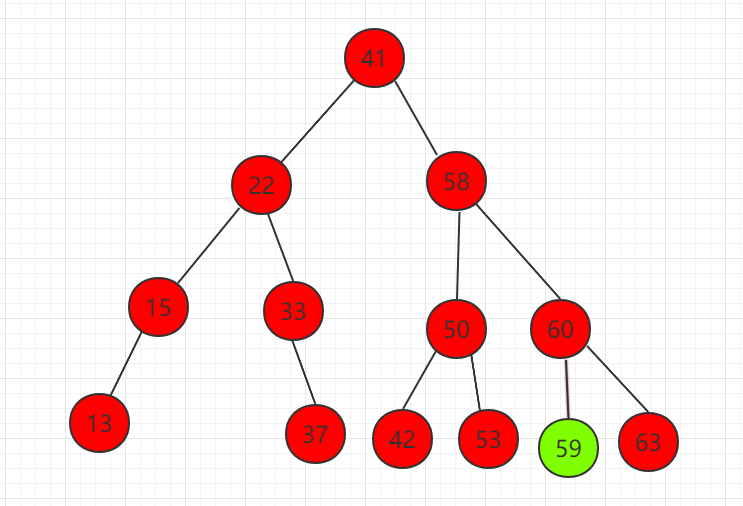
(2)节点 59 代替待删除节点 58
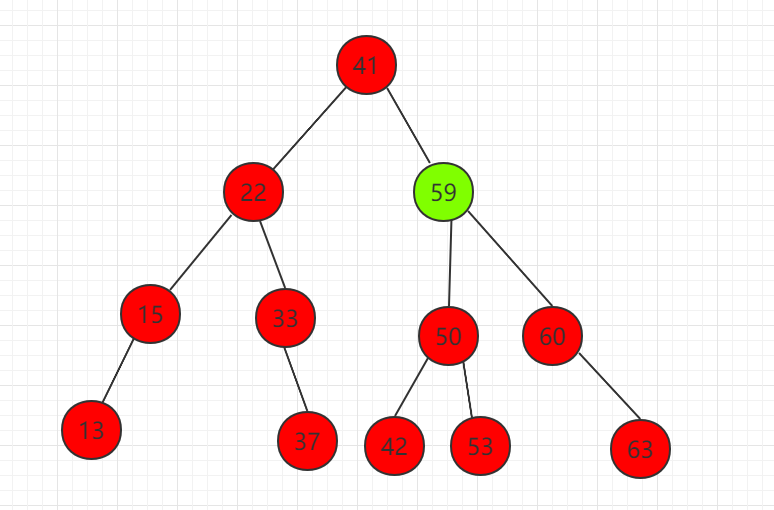
Based on the above rules, delete the node whose key value is key in the binary search tree with node as the root, and the core code example:
源码包下载: Download 5.20.1. Src/runoob/binary/BSTRemove.java file code: ¶
package runoob.binary;
import java.util.LinkedList;
/*\*
\* 二分搜索树节点删除
*/
public class BSTRemove<Key extends Comparable<Key>, Value> {
// 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
private class Node {
private Key key;
private Value value;
private Node left, right;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
left = right = null;
}
public Node(Node node){
this.key = node.key;
this.value = node.value;
this.left = node.left;
this.right = node.right;
}
}
private Node root; // 根节点
private int count; // 树种的节点个数
// 构造函数, 默认构造一棵空二分搜索树
public BSTRemove() {
root = null;
count = 0;
}
// 返回二分搜索树的节点个数
public int size() {
return count;
}
// 返回二分搜索树是否为空
public boolean isEmpty() {
return count == 0;
}
// 向二分搜索树中插入一个新的(key, value)数据对
public void insert(Key key, Value value){
root = insert(root, key, value);
}
// 查看二分搜索树中是否存在键key
public boolean contain(Key key){
return contain(root, key);
}
// 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
public Value search(Key key){
return search( root , key );
}
// 二分搜索树的前序遍历
public void preOrder(){
preOrder(root);
}
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 二分搜索树的后序遍历
public void postOrder(){
postOrder(root);
}
// 二分搜索树的层序遍历
public void levelOrder(){
// 我们使用LinkedList来作为我们的队列
LinkedList<Node> q = new LinkedList<Node>();
q.add(root);
while( !q.isEmpty() ){
Node node = q.remove();
System.out.println(node.key);
if( node.left != null )
q.add( node.left );
if( node.right != null )
q.add( node.right );
}
}
// 寻找二分搜索树的最小的键值
public Key minimum(){
assert count != 0;
Node minNode = minimum( root );
return minNode.key;
}
// 寻找二分搜索树的最大的键值
public Key maximum(){
assert count != 0;
Node maxNode = maximum(root);
return maxNode.key;
}
// 从二分搜索树中删除最小值所在节点
public void removeMin(){
if( root != null )
root = removeMin( root );
}
// 从二分搜索树中删除最大值所在节点
public void removeMax(){
if( root != null )
root = removeMax( root );
}
// 从二分搜索树中删除键值为key的节点
public void remove(Key key){
root = remove(root, key);
}
//*******************\*
//\* 二分搜索树的辅助函数
//*******************\*
// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
// 返回插入新节点后的二分搜索树的根
private Node insert(Node node, Key key, Value value){
if( node == null ){
count ++;
return new Node(key, value);
}
if( key.compareTo(node.key) == 0 )
node.value = value;
else if( key.compareTo(node.key) < 0 )
node.left = insert( node.left , key, value);
else // key > node->key
node.right = insert( node.right, key, value);
return node;
}
// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
private boolean contain(Node node, Key key){
if( node == null )
return false;
if( key.compareTo(node.key) == 0 )
return true;
else if( key.compareTo(node.key) < 0 )
return contain( node.left , key );
else // key > node->key
return contain( node.right , key );
}
// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
private Value search(Node node, Key key){
if( node == null )
return null;
if( key.compareTo(node.key) == 0 )
return node.value;
else if( key.compareTo(node.key) < 0 )
return search( node.left , key );
else // key > node->key
return search( node.right, key );
}
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder(Node node){
if( node != null ){
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder(Node node){
if( node != null ){
inOrder(node.left);
System.out.println(node.key);
inOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder(Node node){
if( node != null ){
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
if( node.left == null )
return node;
return minimum(node.left);
}
// 返回以node为根的二分搜索树的最大键值所在的节点
private Node maximum(Node node){
if( node.right == null )
return node;
return maximum(node.right);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
private Node removeMax(Node node){
if( node.right == null ){
Node leftNode = node.left;
node.left = null;
count --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
// 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
Node remove(Node node, Key key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove( node.left , key );
return node;
}
else if( key.compareTo(node.key) > 0 ){
node.right = remove( node.right, key );
return node;
}
else{ // key == node->key
// 待删除节点左子树为空的情况
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
// 待删除节点右子树为空的情况
if( node.right == null ){
Node leftNode = node.left;
node.left = null;
count--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点,
即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = new Node(minimum(node.right));
count ++;
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
count --;
return successor;
}
}
}