The previous section introduced and looked up size-based optimizations, but there are also some problems in some scenarios, as shown in the following figure, manipulating union (4mem2).
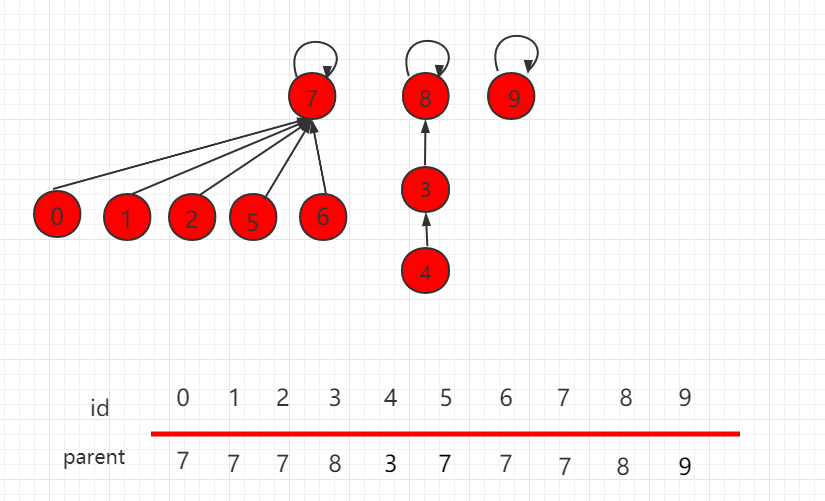
According to the previous section, the optimization of size, the root node of the collection with fewer elements points to the root node with more elements. After the exercise, the number of layers becomes 4, which is one more than before, as shown in the following figure:
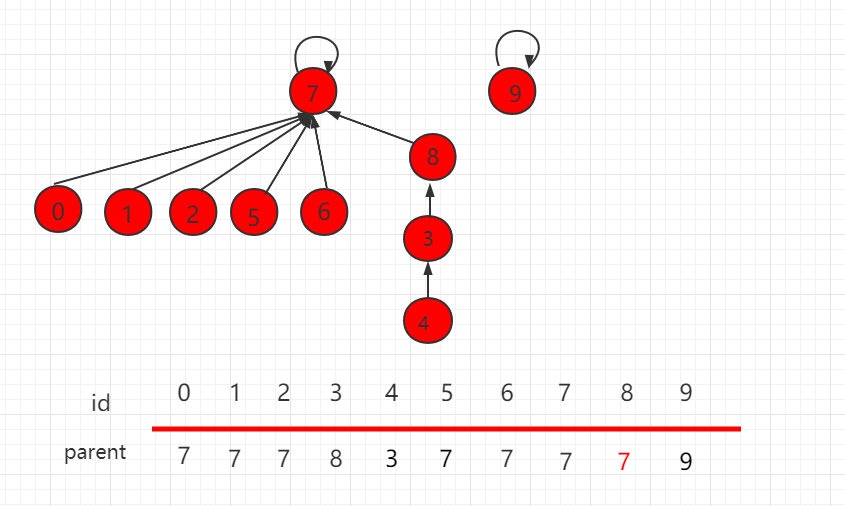
It can be seen that it is not completely correct to rely on the size of the set to judge the direction of the root node according to the number of layers of the two sets. The root node of the set with fewer layers points to the root node of the set with more layers. As shown in the following figure, this is the optimization based on rank.
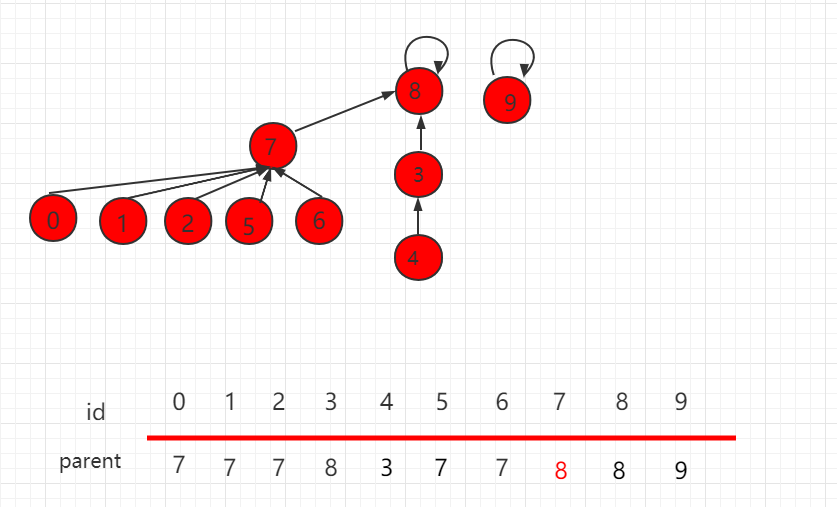
We add the rank array, rank, in the properties of the lookup set. [i] Represents the number of layers of the tree represented by the I-rooted set.
...
private int[] rank; // rank[i]表示以i为根的集合所表示的树的层数
private int[] parent; // parent[i]表示第i个元素所指向的父节点
private int count; // 数据个数
...
The constructor is modified accordingly:
...
// 构造函数
public UnionFind4(int count){
rank = new int[count];
parent = new int[count];
this.count = count;
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for( int i = 0 ; i < count ; i ++ ){
parent[i] = i;
rank[i] = 1;
}
}
...
When merging two elements, you need to compare the number of layers of the root node set, the whole process is O (h) complexity, h is the height of the tree.
...
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
if( rank[pRoot] < rank[qRoot] ){
parent[pRoot] = qRoot;
}
else if( rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
else{ // rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot] += 1; // 此时, 我维护rank的值
}
}
...
5.26.1. Java instance code ¶
源码包下载: Download UnionFind3.java file code: ¶
package runoob.union;
/*\*
\* 基于rank的优化
*/
public class UnionFind4 {
private int[] rank; // rank[i]表示以i为根的集合所表示的树的层数
private int[] parent; // parent[i]表示第i个元素所指向的父节点
private int count; // 数据个数
// 构造函数
public UnionFind4(int count){
rank = new int[count];
parent = new int[count];
this.count = count;
// 初始化, 每一个parent[i]指向自己,
表示每一个元素自己自成一个集合
for( int i = 0 ; i < count ; i ++ ){
parent[i] = i;
rank[i] = 1;
}
}
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p){
assert( p >= 0 && p < count );
// 不断去查询自己的父亲节点, 直到到达根节点
// 根节点的特点: parent[p] == p
while( p != parent[p] )
p = parent[p];
return p;
}
// 查看元素p和元素q是否所属一个集合
// O(h)复杂度, h为树的高度
public boolean isConnected( int p , int q ){
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
// O(h)复杂度, h为树的高度
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
if( rank[pRoot] < rank[qRoot] ){
parent[pRoot] = qRoot;
}
else if( rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
else{ // rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot] += 1; // 维护rank的值
}
}
}