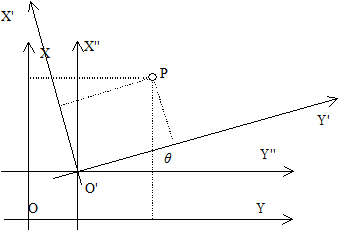
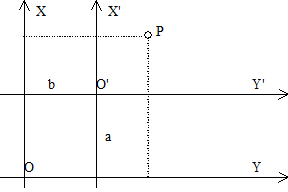
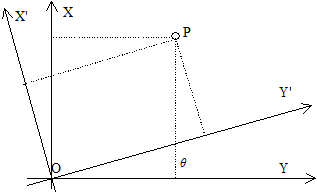
The so-called coordinate system includes two aspects: one is the size of the ellipsoid used in calculating of the measurement results on the geoid to the surface of the ellipsoid; the other is that the relative positions of the ellipsoid and the geoid are different, and the results calculated on the geographic coordinates of the same point will have different values. Therefore, a certain size ellipsoid is selected and its position with the geoid is determined, so a coordinate system is determined (Fig. 4-3). Fig. 49 Relationship between the real world and coordinate space # In addition to revolving around the sun, the earth revolves around its own axis. The axis of rotation coincides with the short axis of the ellipsoid and intersects with the ground at two points, namely, the two poles of the earth, the North Pole and the South Pole. The plane perpendicular to the earth’s axis and passing through the earth’s center is called the equatorial plane, and the large circle (intersection line) intersecting the equatorial plane with the earth’s surface is called the equator. The circles parallel to the equator are called the parallels. Obviously, the equator is the largest latitude circle. The plane passing through the Earth’s axis and perpendicular to the equatorial plane is called a meridian plane or geographic meridian. All geographic meridians are equal in length. (Figure 4-4) Fig. 50 Meridians and parallels of the Earth # Let there be a point P (Fig. 4-4) on the ellipsoid surface, and make the vertical line of the ellipsoid through the point P, which is called the normal line passing through the point P. The angle between the normal line and the equatorial plane, called the geographic latitude of point P (referred to as latitude), is usually written in letters φ . Latitude starts from the equator, and is 0 on the equator. The farther the latitude is from the equator, the greater the latitude is, and the latitude to the pole is 90 degrees. To the north of the equator is called the northern latitude, and to the south is called the southern latitude. The dihedral angle between the meridian plane passing through point P and the meridian plane passing through Greenwich Observatory is called the geographic longitude of point P (longitude for short), which is usually expressed by the letter lambda. According to international regulations, the meridian of Greenwich Observatory is the primary meridian (or the first meridian) as the starting point of longitude calculation. The longitude of this line is 0 degrees, 0-180 degrees to the East is called the East meridian, and 0-180 degrees to the west is called the West meridian. The position of any point on the ground is usually determined by longitude and latitude. Longitudinal and latitudinal lines are two sets of orthogonal (intersection 90 degree) curves on the surface of the earth. The coordinates formed by these two sets of orthogonal curves are called geographic coordinate systems. The difference of longitude between two points on the surface is called longitude difference, and the difference of latitude between two points is called latitude difference. For example, the geographical position of Beijing can be defined as 39°56’ North latitude and 116°24’ East longitude. Geographic coordinates are a type of spherical coordinates. Since the Earth’s surface is a non-developable surface, meaning points on the surface cannot be directly represented on a plane, it is necessary to apply map projection methods to establish a functional relationship between points on the Earth’s surface and points on a plane. This ensures that for any point on the Earth’s surface defined by geographic coordinates (φ, λ) , there is always a corresponding point on the plane. The position of any point on the plane can be expressed using polar coordinates or rectangular coordinates. Select a point O on the plane as the origin of the rectangular coordinate system, and establish a plane rectangular coordinate system by drawing two mutually perpendicular axes, X’OX and Y’OY , passing through point O , as shown in Figure 5. In the rectangular coordinate system, the OX and OY directions are defined as positive, while the OX and OY directions are defined as negative. Thus, the position of a given point P in the coordinate system can be uniquely determined by the lengths of the perpendiculars from the point to the OX and OY axes, i.e., x = AP and y = BP , generally denoted as P(x, y) . Fig. 51 The plane rectangular coordinate system and the polar coordinate system # As shown in Figure 5, let O’ be the origin of the polar coordinate system and O’O be the polar axis. If P is a point in the coordinate system, then O’P is called the polar radius, denoted by the symbol ρ , i.e., ρ = O’P. ∠OO’P is the polar angle, denoted by the symbol δ , i.e., ∠OO’P = δ . The polar angle δ is measured from the polar axis, with counterclockwise direction taken as positive and clockwise direction as negative. A relationship can be established between polar coordinates and plane rectangular coordinates. As can be seen from Figure 5, the x-axis of the rectangular coordinate system coincides with the polar axis, and the distance between the origins of the two coordinate systems, OO’ , is denoted by Q . Thus, the following holds: X=Q–ρcosδ Y=ρsinδ As shown in Figure 4-6, the corresponding axes of coordinate system XOY and coordinate system X’O’Y’ are parallel to each other and share the same positive direction. Coordinate system X’O’Y’ is obtained by translating coordinate system XOY parallelly. Let the coordinates of point P in coordinate system XOY be (x, y) , and its coordinates in X’O’Y’ be (x’, y’) , while (a, b) are the coordinates of O’ in coordinate system XOY . Then: x=x’ +a y=y’ +b The former is the coordinate relation of a point before and after the translation of the coordinate system。 Fig. 52 Coordinate system translation # As shown in Figure 4-7, the origin of coordinate system XOY coincides with that of coordinate system X’O’Y’ , and the angle between their corresponding coordinate axes is θ . The coordinate system X’O’Y’ is obtained by rotating the coordinate system XOY counterclockwise around point O by an angle of θ . x=x’cosθ+y’sinθ y=y’cosθ-x’sinθ The above formula is the relationship of coordinates of a point in the two-rectangular coordinate system after rotating of the θ angle. Fig. 53 Coordinate system rotation # As shown in Figure 4-8, the origin of coordinate system X’O’Y’ has coordinates a and b in coordinate system XOY , and the angle between the X -axis and the X’ -axis is θ . It can be considered that coordinate system X’O’Y’ originally coincided with coordinate system XOY , and was then translated by distances a and b to point O’ , after which the coordinate axes O’X’ and O’Y’ were rotated counterclockwise by an angle θ relative to OX and OY . Introduce an auxiliary coordinate system X”O’Y” between the two coordinate systems, such that its coordinate axes O’X” and O’Y” are parallel to OX and OY , respectively. If a point P in the X”O’Y” system has coordinates (x”, y”) , then the following can be derived using the coordinate translation and rotation formulas: x=x”+a y=y”+b Thus x”=x’cosθ+y’sinθ y”=y’cosθ-x’sinθ That is, x=x’cosθ+y’sinθ+a y”=y’cosθ-x’sinθ+b The above formula represents the relationship between the coordinates of a point in the new and old coordinate systems after translation and rotation. Fig. 54 Translation and rotation of coordinate system # 
Geographic coordinates #
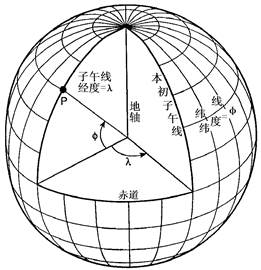
Latitude #
Longitude #
Determination of points on the ground #
Coordinate system on the plane #
Establishment of plane rectangular coordinate system #
Establishment of Polar Coordinate System #

Translation and rotation of rectangular coordinate system #
Coordinate system translation #
Coordinate system rotation #
Translation and rotation of coordinate system #